EGMO 2024 | Problem 2 | Solution - 13 April 2024

Problem 2. Let ABC be a triangle with AC > AB , and denote its circumcircle by Ω and incentre by I . Let its incircle meet sides BC, CA, AB at D, E, F respectively. Let X and Y be two points on minor arcs

\overset{⏜}{D F}

and

\overset{⏜}{D E}

of the incircle, respectively, such that ∠ BXD = ∠ DYC . Let line XY meet line BC at K . Let T be the point on Ω such that KT is tangent to Ω and T is on the same side of line BC as A . Prove that lines TD and AI meet on Ω.

Solution 1

Invert about a circle centred at $D$ with radius $\sqrt{DB\cdot DC}$ , followed by a flip about $D$ . The incircle is sent to a parallel line to $BC$ , and $\Omega$ is fixed by Power of a Point. Now the angle condition is reformulated as $\angle DCX'=\angle DBY'$ , but since $X',Y'$ lie on a parallel line to $BC$ , $Y'BCX'$ is an isosceles trapezium.

Now as the center of $(Y'DX')$ lies on the perpendicular bisector of $X'Y'$ as it is a chord, by symmetry $K'=(Y'DX')\cap BC$ is the reflection of $D$ about the midpoint of $BC$ . In fact, $(DK'T')$ being tangent to $\Omega$ , implies $T'$ is the arc midpoint of $BC$ as the tangency point is fixed about a reflection across the perpendicular bisector of $BC$ (Else we would have two intersection points of $(DK'T')$ with $\Omega$ ), and $D,K'$ swap under this reflection.

In fact as $\Omega$ is fixed $T'=TD\cap \Omega$ , but as it is the arc midpoint by the Incenter-Excenter Lemma $A,I,T'$ are collinear and we are done,

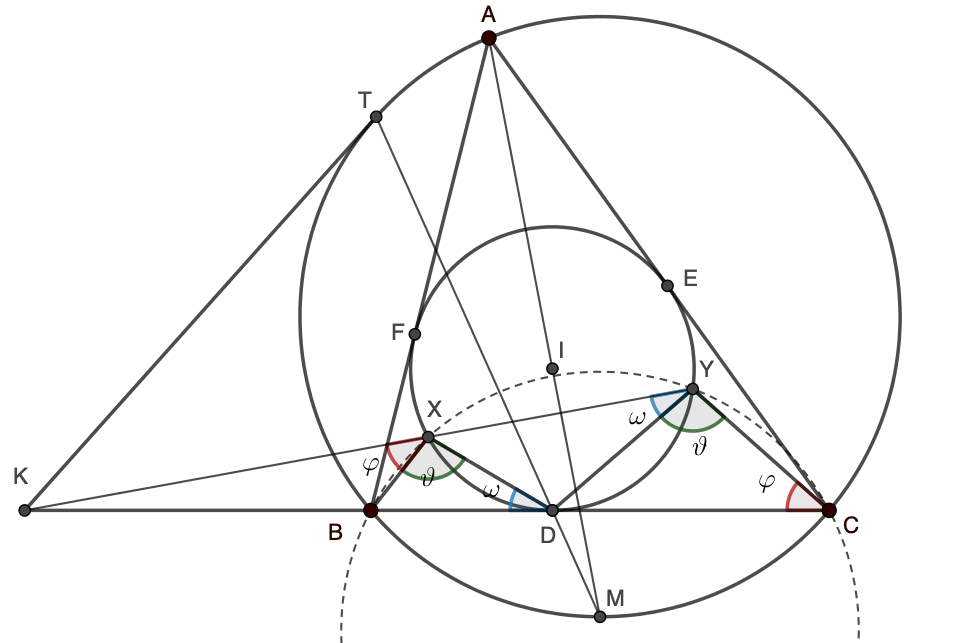
Solution 2

Let $\vartheta=\angle BXD=\angle DYC$ , $\omega=\angle KYD=\angle XDB$ , and $k=\angle YKC=\angle XKD$ .

We first note that quadrilateral $BXYC$ is cyclic, since $\angle KBX=\angle BXD+\angle BDX=\angle XYC$ . So, also let $\varphi=\angle KXB=\angle YCD$ .

Since $KD$ is tangent to the incircle of $\triangle ABC$ and $KT$ is tangent to $\Omega$ at $T$ , from the power of point theorem we get
$KD^2=KX\cdot KY=KB\cdot KC=KT^2,$ and so $KD=KT$ .
From triangles $\triangle KXD$ and $\triangle KYC$ we have
$\frac{KX}{XD}=\frac{\sin\omega}{\sin k}. \quad \text{and}\quad \frac{KY}{YC}=\frac{\sin \varphi}{\sin k}.$ By the ratio lemma, we have
$\frac{KB}{BD}=\frac{KX}{XD}\cdot \frac{\sin \varphi}{\sin \theta}=\frac{\sin\omega}{\sin k}\cdot \frac{\sin \varphi}{\sin \theta}$ and
$\frac{KD}{DC}=\frac{KY}{YC}\cdot \frac{\sin \omega}{\sin \theta}=\frac{\sin \varphi}{\sin k}\cdot \frac{\sin \omega}{\sin \theta}$ Hence $\frac{KD}{DC}=\frac{KB}{BD}$ , and so,
$\frac{KD}{KB}=\frac{DC}{BD}.$
Also, triangles $\triangle KTB$ and $\triangle KCT$ are similar, since $\angle KTB= \angle BCK$ , so
$\frac{TC}{TB}=\frac{KT}{KB}=\frac{KD}{KB}=\frac{DC}{BD}.$ Therefore, $TD$ bisects angle $\angle BTC$ , and so $TD$ and $AI$ , as the angle bisector of $\angle BAC$ , meet at the midpoint $M$ of arc $BC$ .